TEMA 11: SEMEJANZA
PROGRAMACIÓN
PROGRAMACIÓN
Ses. | Metodología |
1ª / | - Explicar el concepto de semejanza. - Cómo construir figuras semejantes. - Ejerc.: Pág. 217 (1, 3 y 4). |
2ª / | - Corregir sesión anterior. - Explicar escalas, cálculo con escalas, planos y mapas, ampliación y reducción. - Ejercicios: Pág. 221 (12 a 16) . |
3ª / | - Corregir sesión anterior. - Relación entre longitudes, áreas y volúmenes de figuras semejantes. - Ejercicios: Pág. 221 (10), 224 (32 y 33). |
4ª / | - Corregir sesión anterior. - Explicar el teorema de Thales y construcción de segmentos proporcionales. - Ejercicios: Pág. 219 (5 y 9) y 224 (27). |
5ª / | - Corregir sesión anterior. - Semejanza de triángulos y triángulos en posición de Tales. - Ejercicios: Pág. 219 (7 y 8), 224 (29 a 31). Aprender los criterios de semejanza de triángulos. |
6ª / | - Corregir sesión anterior. - Teorema de Pitágoras, de la altura y del cateto. - Ejercicios: Pág. 223 (17 a 23). |
7ª / | - Corregir sesión anterior. - Estudiar y repasar. |
8ª / | - CONTROL. |
TEMA 11: SEMEJANZA
Figuras semejantes: Dos figuras son semejantes cuando
- Tienen la misma forma [y, por lo tanto, sus ángulos son iguales].
- Sus lados son proporcionales: los de una figura se obtienen multiplicando a los de la otra por un número fijo, llamado razón de semejanza (r).
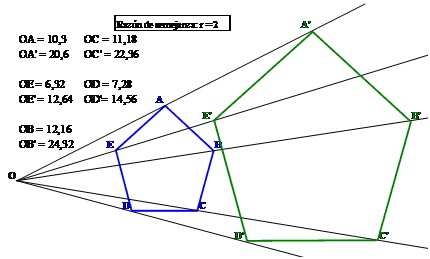
La razón de semejanza del cuadrado verde con respecto al azul es: r = 2.
Al ser proporcionales se puede establecer entre ellos las siguientes proporciones:
a) Del cuadrado verde con respecto al azul. Las razones de sus lados forman esta proporción:
b) Del cuadrado azul con respecto al verde. Las razones de sus lados forman esta proporción:
Cómo construir figuras semejantes
a) Mediante cuadrícula:
- Se cuadricula la figura original.
- Se dibuja una cuadrícula con la longitud de sus cuadros igual a la longitud de los cuadros originales multiplicada por la razón de semejanza.
- En la nueva cuadrícula se dibuja la figura semejante a la dada, cuidando de que quede situada en los mismos cuadros que la original.
[En este ejemplo la razón de semejanza de la figura grande con respecto a la pequeña es 2]
b) Mediante Proyección:
- Se dibuja un punto cualquiera, al que llamaremos centro de proyección.
- Desde el centro de proyección se trazan semirrectas que pasen por los vértices de la figura original.
- La distancia desde el centro de proyección a cada vértice se multiplica por la razón de semejanza y el resultado será la distancia desde el centro de proyección a los vértices de la figura semejante.
Escala: Relación que hay entre la representación (plano, mapa, etc.) y la realidad. Ej.: La escala 1:50 quiere decir que lo que en la realidad mida 1 (km, m, cm, dm o la unidad que sea) en el plano está dividido por 50. O, lo que es lo mismo, que lo que en el plano mida 1, en la realidad está multiplicado por 50. En definitiva, estamos hablando de figuras semejantes y la escala es lo mismo que la razón de semejanza.
Cálculos con escalas: Es muy práctico tratar los problemas de escalas como si fueran problemas de regla de tres. [Se forman dos columnas con las cabeceras PLANO y REALIDAD y en ellas se colocan adecuadamente los datos de la Escala y del Problema]
a) Cálculo de la medida real:
Ejemplo: ¿Cuánto mide en la realidad una ventana que en un plano de 1:50 mide 3 cm de ancho?
b) Cálculo de la medida en el plano:
Ejemplo: ¿Cuánto mide en un plano de 1:20 una puerta de 80 cm de alto?
c) Cálculo de la escala:
Ejemplo: Entre A y B hay 4.000 m y la distancia en el plano es de 2 cm . ¿Cuál es la escala?
[¡Cuidado con las unidades: han de ser del mismo orden!]
Planos y mapas: Un plano es una representación, generalmente de una construcción, en la que la escala suele ser grande (superior a 1:10 000) [Para que la escala sea superior a 1:10000 se ha de disminuir el divisor]. La escala de los planos suele oscilar desde 1:50 a 1:200.
Un mapa es una representación de grandes superficies en la que la escala suele ser pequeña (inferior a 1:10 000). [Cuanto mayor sea el denominador, menor será el resultado, o sea, más pequeña será la escala]. La escala de los mapas suele ir de 1:300 000 a 1:25 000 000. [Los del ejército suelen ser de escala inferior (del orden de 1:50 000); los mapas catastrales tienen una escala todavía inferior (del orden de 1:1000 o menos)].
Cuando hacemos representaciones a escala de objetos tridimensionales las llamamos maquetas.
Ampliación y reducción: Ampliar o reducir algo es dibujarlo o construirlo a escala. Habitualmente, las ampliaciones y reducciones se expresan en porcentajes. Así, por ejemplo, una ampliación de un 50 % significa que lo que en la realidad mida 100 se convertirá en 150 (100 + 50). La razón de semejanza o escala será de 150/100 = 1,5. Lo mismo ocurre con la reducción: Una reducción de un 20 % significa que lo que en la realidad mida 100 se convertirá en 80 (100-20). La razón de semejanza o escala será de 80/100 = 0,8.
Relaciones entre longitudes, áreas y volúmenes de figuras semejantes:
a) Razón de las longitudes: La razón de semejanza de las longitudes es igual a la razón de semejanza.
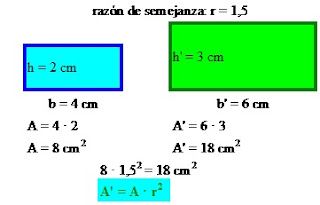
b) Razón de las áreas: La razón de semejanza de las áreas es el cuadrado de la razón de semejanza de los lados [Si la razón de semejanza de los lados es r, el área de la figura semejante se obtiene multiplicando el área de la figura original por r2].
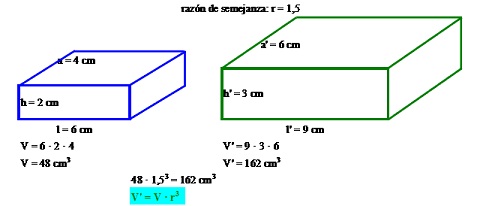
c) Razón de los volúmenes: La razón de semejanza de los volúmenes es el cubo de la razón de semejanza de las aristas [Si la razón de semejanza de las aristas es r, el volumen de la figura semejante se obtiene multiplicando el volumen de la figura original por r3].
TEOREMA DE TALES (Thales) (rectas secantes cortadas por paralelas):
Dadas dos rectas secantes y varias paralelas que las corten, los segmentos que se forman en una secante son proporcionales a los correspondientes en la otra secante.
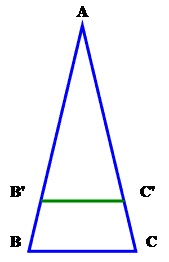
Ejemplo: Si en el dibujo anterior el segmento AB = 2 cm , A’B’ = 3 cm , B’C’ = 6 cm , ¿cuánto mide el segmento BC?
Tales de Mileto [Mileto: antigua ciudad griega que actualmente está en Turquía]: (624 a 547 aC ). Filósofo griego, uno de los siete sabios de Grecia. Se le considera como el creador de la Física , de la Geometría y de la Astronomía y se dice que midió la altura de las pirámides por su sombra, que descubrió alguna de las propiedades del triángulo esférico y que estableció la teoría de los eclipses. Se encuentra entre los primeros que observaron las atracciones y repulsiones del ámbar amarillo al ser frotado por un trozo de lana, base del descubrimiento de la electricidad, y se le atribuye la máxima “gnosce te ipsum” (conócete a ti mismo). Enseñó que el agua es el principio de todas las cosas y que la Tierra es un disco que flota en ella. Tiene fama de haber predicho el eclipse que, transformando el día en noche, suspendió la batalla entablada entre lidios y medas en el año 585, a .C. Viajó mucho, en especial por Egipto, y enseñó a los navegantes griegos a guiarse por la Osa Menor , en vez de la Osa Mayor. [Tomado de Enciclopedia Universal Sopena. Edit. Ramón Sopena. Barcelona, 1974].
Dividir un segmento en partes iguales:
Desde un extremo A del segmento se traza una semirrecta secante s y con el compás se marcan en ella las divisiones que se pidan del tamaño que queramos, pero todas iguales (o sea, sin mover la apertura del compás). Se une la última marca de la secante con el otro extremo B del segmento y luego se trazan paralelas a esta última recta por cada una de las divisiones que habíamos hecho en la secante, con lo cual estas paralelas cortarán al segmento AB y lo dejarán dividido en partes iguales.
Un procedimiento parecido se sigue para dividir un segmento AB en partes proporcionales a otros segmentos dados, salvo que, en este caso, las divisiones en la secante han de ser iguales a los segmentos dados.
Semejanza de triángulos
Dos triángulos son semejantes si tienen sus ángulos iguales y sus lados proporcionales.
Criterios de semejanza de triángulos: Para saber si dos triángulos son semejantes no es necesario comprobar si tienen los tres ángulos iguales y los tres lados proporcionales, basta con comprobar que cumplen alguno de los siguientes criterios:
1.- Dos triángulos son semejantes si tienen dos ángulos iguales.
2.- Dos triángulos son semejantes si tienen un ángulo igual y los dos lados que lo forman son proporcionales.
3.- Dos triángulos son semejantes si tienen los tres lados proporcionales.
Triángulos en posición de Tales
Dos triángulos están en posición de Tales cuando tienen un ángulo común y los lados opuestos a ese ángulo son paralelos. Los triángulos en posición de Tales son semejantes. Dos triángulos semejantes se pueden colocar en posición de Tales.
En los triángulos ABC y AB’C’ tenemos un ángulo común, el A, y los lados BC y B’C’, opuestos al ángulo A, son paralelos.
Por ser triángulos semejantes se establecen entre sus lados la siguiente proporción:
TEOREMA DE PITÁGORAS
En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos: h2 = c12 + c22. [¡OJO! La correcta expresión de la redacción de esta fórmula suele acarrear problemas a los alumnos, sobre todo en el orden de las palabras “suma”, “cuadrados” y “catetos”].
De la fórmula de la hipotenusa se deducen, por ecuaciones, las fórmulas de los catetos:
c12 = h2 – c22
c22 = h2 – c12
Aplicación: En un triángulo rectángulo sus catetos miden 3 cm y 4 cm . ¿Cuánto mide su hipotenusa?
Aplicación: En un triángulo rectángulo la hipotenusa mide 13 cm y uno de sus catetos mide 12 cm . ¿Cuánto mide el otro cateto?
Teorema de la altura en un triángulo rectángulo
En un triángulo rectángulo el cuadrado de la altura sobre la hipotenusa es igual al producto de los dos segmentos que determina sobre la hipotenusa.
a2 = b1 · b2
Teorema del cateto en un triángulo rectángulo
En un triángulo rectángulo el cuadrado de un cateto es igual al producto de la hipotenusa por la proyección del cateto sobre la misma.
c12 = h · b1
Ternas pitagóricas: Conjunto de tres números que cumplen el teorema de Pitágoras.
Ejemplo: 3, 4 y 5 (triángulo egipcio); 5, 12 y 13. Si tres números forman una terna pitagórica, sus múltiplos también.